↓Skip to main content

3-D Segmentation of Brain MRIs

·
Artificial Intelligence Coursework 3-D Segmentation Medical Imaging Perception Stanford CS
James Braza
James Braza
Artificial Intelligence and Software
Table of Contents
Convolutional U-Net models can be trimmed and tuned to fit on miniature computers, enabling real-time inference within medical devices.

Introduction
#

In spring 2023, I took CS231n: Deep Learning for Computer Vision at Stanford. My group of three chose to explore volumetric (“3-D”) segmentation of MRI images. Using 2020 data from the University of Pennsylvania’s Brain Tumor Segmentation (BraTS) Challenge, we trained and experimented with multiple U-Net architectures.

The dataset consisted of 369 labelled examples each containing 5 MRIs:

  • Four input scans: T2 FLAIR, T1, T1 contrast enhanced, T2
  • One mask of four classes: non-tumor (0b000), non-enhancing tumor core (0b001), peritumoral edema (0b010), and Gadolinium-enhancing tumor (0b100)
MRI cross-section showing U-Net performance
A 3-D U-Net was input four MRI scans (top) and segmented to tumor classes. This cross-section shows target mask (left) and binarized predictions (right).

U-Net Architecture
#

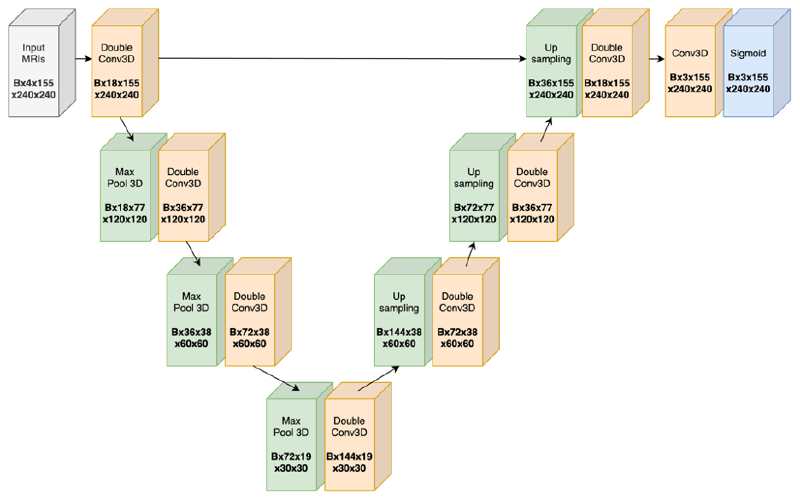
Diagram of our U-Net architecture with 3-D convolutions
The U-Net architecture is named for its U-shaped encoder-decoder structure, we used 4 or 5 levels. The sigmoid’s output is binarized in post-processing for predictions, and the binary threshold is a hyperparameter.

One can choose to use 3-D or 2-D convolutions in the U-Net:

  • 3-D convolution: can directly intake a 3-D MRI and leverage 3-D spatial information, at the cost of 3X more weights
  • 2-D convolution: an MRI now becomes a list of 2-D images, so to process an MRI the model is internally doing a nested for loop

We experimented with both 2-D and 3-D convolutions.

One note is, because the output of the sigmoid is logits, the loss function used was the equally-weighted sum of binary cross entropy (with logits) loss and Dice loss.

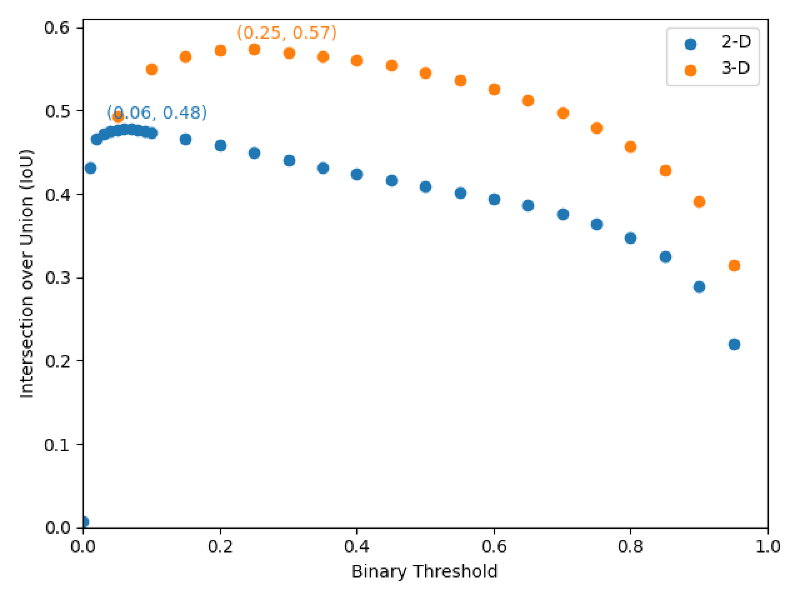
Binary Threshold Tuning
#

Figure showing a sweep over possible binary thresholds
We swept across possible global binary thresholds, computing the metric intersection over union (IoU) on our validation set, to optimize the threshold. We can see the 2-D and 3-D convolutions require different thresholds, and 3-D convolutions attain an almost universally higher IoU.

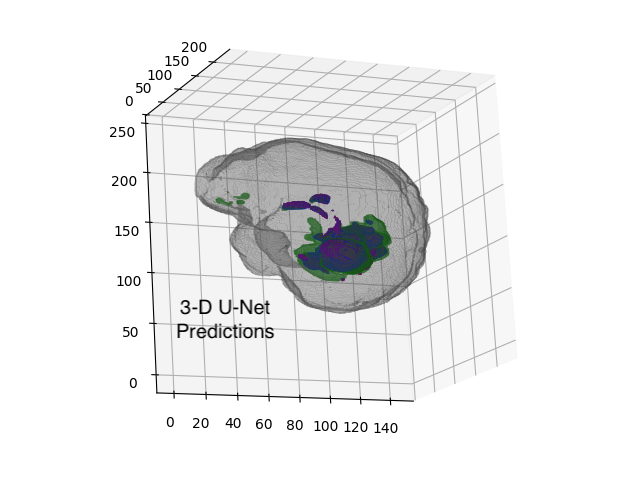
Other Findings
#

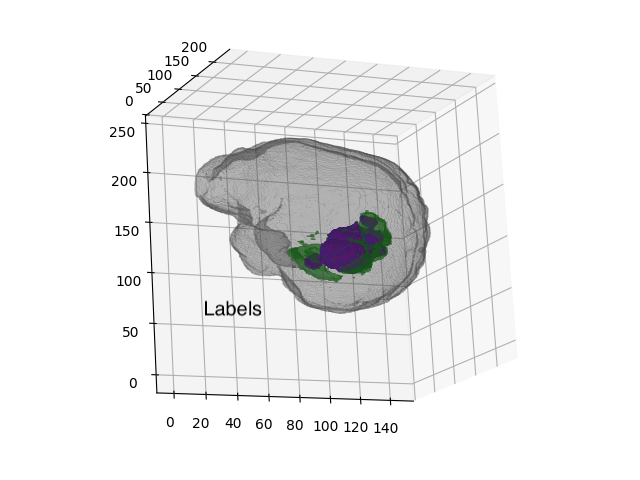
  • 3-D convolutional layers outperform 2-D layers, indicating 3-D U-Nets are actually leveraging 3-D spatial information
  • Applying one global binary threshold to convert raw predictions to class predictions is equally performant as per-mask binary thresholding
  • Global parameter pruning, encoder-decoder pair pruning, and reducing weight precision (float32 to float16) were effective methods of reducing model size without hampering performance

Source Code
#

jamesbraza/cs231n-3d-segmentation

Stanford CS231N Deep Learning for Computer Vision Class Project

Python
0
0