↓Skip to main content

DreamChess: Chess-Playing AI

·
Artificial Intelligence Coursework Chess AI Offline Learning Reinforcement Learning Stanford CS
James Braza
James Braza
Artificial Intelligence and Software
Table of Contents
AlphaGo Zero-style chess-playing AI with our own chess state-action embedding technique.

In winter 2023, I took CS234: Reinforcement Learning at Stanford. We found no open source AlphaGo Zero-style chess AI with available weights existed, so we sought to be the first (and explore recreating the AlphaGo Zero paper simultaneously).

Chess Representation
#

To get started quickly, we assumed a conservative action space \( |A| = 64^2 = 4096 \) moves and no pawn underpromotion (only queen promotions), and on any given turn constrained our probability distribution to valid moves.

Game state was a two-tuple of chess Board object and player ID (white or black). We “canonicalized” the board view, meaning the board was flipped if the black player, so the network always had the same perspective (bottom looking up). We also mirrored the board + player to store two training examples per self-play move. Lastly, we used a library python-chess to handle all chess-specific rules.

Diagram of signed board embedding
Our signed one-hot Board embedding used one board per piece (0: pawn, 1: knight, 2: bishop, 3: rook, 4: queen, 5: king), with elements being 1 for white piece, -1 for black piece, and 0 for no piece. Thus, the signed embedding has shape 6 x 8 x 8. An alternate unsigned one-hot embedding uses 12 boards containing only 0 or 1, giving players separate boards.

Architecture Versions
#

Both versions of our architecture adhered to the same signature:

  • Input: Batch of board embeddings of shape \( (B, D, H, W) \)
    • D = 6 (signed embedding) or 12 (unsigned embedding)
  • Policy head output: batch of policy distributions of shape \( (B, |A|) \)
  • Value head output: batch of values of shape \( (B, 1) \)

Training matched the AlphaZero paper:

  • Reward: 1 for win, -1 for loss, 0 if ongoing, \( 10^{-5} \) for tie
  • Loss: sum of cross-entropy loss on the policy head, mean squared error loss on the value head, and L2 regularization
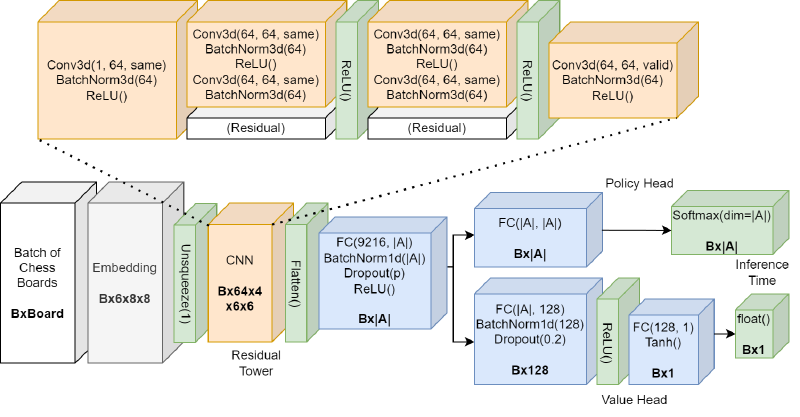
Diagram of our v1 network architecture
The v1 network has a residual tower of 3-D convolutions, and both a policy and value head.
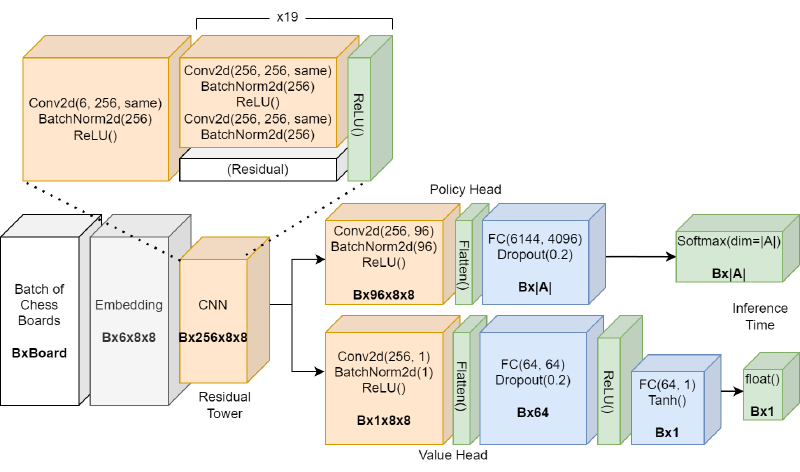
Diagram of our v2 network architecture
The v2 network moves to 2-D convolutions to avoid convolving piece types (thus preserving piece differences), added dropout to combat policy head overfitting, and vastly shrinks the network to match the AlphaGo Zero’s paper’s hyperparameters.

Findings
#

  • Embedding pieces into an unsigned 12 x 8 x 8 matrix demonstrated superior gameplay over a signed 6 x 8 x 8 matrix, at the expense of training time
  • Our v2 network was superior to our v1 network when using the same piece embedding
  • Both the v1 and v2 networks could beat a random player, but neither were able to beat a 1350 Elo Stockfish engine player

Source Code
#

jamesbraza/cs234-dreamchess

Stanford CS234 Reinforcement Learning Class Project

Python
0
0